Yin's Blog
0%

60行NumPy手搓GPT[翻译]

Posted on Edited on

本文还是来自Jay Mody，那篇被Andrej Karpathy手动点赞的GPT in 60 Lines of NumPy。

LLM大行其道，然而大多数GPT模型都像个黑盒子一般隐隐绰绰，甚至很多人都开始神秘化这个技术。我觉得直接跳进数学原理和代码里看看真实发生了什么，才是最有效的理解某项技术的方法。正如DeepMind的Julian Schrittwieser所说：

这些都是电脑程序。

这篇文章细致的讲解了GPT模型的核心组成及原理，并且用Numpy手搓了一个完整的实现（可以跑的那种），读起来真的神清气爽。项目代码也完全开源，叫做picoGPT(pico，果然是不能再小的GPT了)。

原文链接：GPT in 60 Lines of NumPy

译文链接：60行NumPy手搓GPT

(已获原文作者授权)

关于译文几点说明：

  • 翻译基本按照原作者的表述和逻辑，个别部分译者做了补充和看法；
  • 文中的个别英文术语很难翻译，算是该领域的专有名词了，因此这类术语就直接保留了，比如transformer

在本文中，我们将仅仅使用60行Numpy，从0-1实现一个GPT。然后我们将OpenAI发布的GPT-2模型的权重加载进我们的实现并生成一些文本。

注意：

  • 本文假定读者熟悉Python，Numpy，还有一些训练神经网络的基本经验。

  • 考虑到在保持完整性的同时让实现尽可能的简单，本文的实现故意丢弃了原始模型的大量功能和特点。目的很简单啊，就是提供一个简单且完整的GPT的技术介绍，作为教学用途使用。

  • GPT架构只是LLM取得今时今日成就的一个小小组成部分[1]

  • 本文中的所有代码都可以在这里找到:https://github.com/jaymody/picoGPT

  • Hacker news上关于本文的讨论

更新(2023/2/9)：添加了”下一步呢？”部分，并且更新了介绍部分

更新(2023/2/28)：为“下一步呢？”部分又添加了一些内容

GPT是什么?

GPT代表生成式预训练Transformer(Generative Pre-trained Transformer)。这是一类基于transformer的神经网络架构。Jay Alammar的”GPT3是如何工作的”一文在宏观视角下对GPT进行了精彩的介绍。但这里简单来说：

  • 生成式(Generative)：GPT可以生成文本
  • 预训练(Pre-trained)：GPT基于来自于书本、互联网等来源的海量文本进行训练
  • Transformer：GPT是一个decoder-only的transformer神经网络结构

    译者注：Transformer就是一种特定的神经网络结构

类似OpenAI的GPT-3, 谷歌的LaMDA还有Cohere的Command XLarge的大语言模型的底层都是GPT模型。让它们这么特殊的原因是1）它们非常的大（成百上千亿的参数）；2）它们是基于海量数据进行训练的（成百上千个GB的文本数据）

根本上来看，给定一组提示，GPT能够基于此生成文本。即使是使用如此简单的API（input = 文本，output = 文本），一个训练好的GPT能够完成很多出色的任务，比如帮你写邮件，总结一本书，给你的instagram起标题，给5岁的小孩解释什么是黑洞，写SQL代码，甚至帮你写下你的遗嘱。

以上就是宏观视角下关于GPT的概览以及它能够做的事情。现在让我们深入一些细节把。

输入/输入

一个GPT的函数签名基本上类似这样：

1
2
3
4
5
def gpt(inputs: list[int]) -> list[list[float]]:
    # inputs has shape [n_seq]
    # output has shape [n_seq, n_vocab]
    output = # beep boop neural network magic
    return output

输入

输入是一些文本，这些文本被表示成一串整数序列，每个整数都与文本中的token对应：

1
2
3
4
# integers represent tokens in our text, for example:
# text   = "not all heroes wear capes":
# tokens = "not"  "all" "heroes" "wear" "capes"
inputs =   [1,     0,    2,      4,     6]

token是文本的小片段，它们由某种分词器（tokenizer）产生。我们可以通过一个词汇表(vocabulary)将tokens映射为整数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# the index of a token in the vocab represents the integer id for that token
# i.e. the integer id for "heroes" would be 2, since vocab[2] = "heroes"
vocab = ["all", "not", "heroes", "the", "wear", ".", "capes"]

# a pretend tokenizer that tokenizes on whitespace
tokenizer = WhitespaceTokenizer(vocab)

# the encode() method converts a str -> list[int]
ids = tokenizer.encode("not all heroes wear") # ids = [1, 0, 2, 4]

# we can see what the actual tokens are via our vocab mapping
tokens = [tokenizer.vocab[i] for i in ids] # tokens = ["not", "all", "heroes", "wear"]

# the decode() method converts back a list[int] -> str
text = tokenizer.decode(ids) # text = "not all heroes wear"

简单说：

  • 我们有一个字符串
  • 我们使用tokenizer将其拆解为小片段-我们称之为token
  • 我们使用词汇表将这些token映射为整数

在实际中，我们不仅仅使用简单的通过空白分隔去做分词，我们会使用一些更高级的方法，比如Byte-Pair Encoding或者WordPiece，但它们的原理是一样的：

  1. 有一个vocab即词汇表，可以将字符串token映射到整数索引
  2. 有一个encode方法，即编码方法，可以实现str -> list[int]的转化
  3. 有一个decode方法，即解码方法，可以实现list[int] -> str的转化[2]

输出

输出是一个二维数组，其中output[i][j]表示模型的预测概率，这个概率代表了词汇表中位于vocab[j]的token是下一个tokeninputs[i+1]的概率。比如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
vocab = ["all", "not", "heroes", "the", "wear", ".", "capes"]
inputs = [1, 0, 2, 4] # "not" "all" "heroes" "wear"
output = gpt(inputs)
#              ["all", "not", "heroes", "the", "wear", ".", "capes"]
# output[0] =  [0.75    0.1     0.0       0.15    0.0   0.0    0.0  ]
# 在"not"给出的情况下，我们可以看到，(对于下一个token)模型预测"all"具有最高的概率

#              ["all", "not", "heroes", "the", "wear", ".", "capes"]
# output[1] =  [0.0     0.0      0.8     0.1    0.0    0.0   0.1  ]
# 在序列["not", "all"]给出的情况下，(对于下一个token)模型预测"heroes"具有最高的概率

#              ["all", "not", "heroes", "the", "wear", ".", "capes"]
# output[-1] = [0.0     0.0     0.0     0.1     0.0    0.05  0.85  ]
# 在整个序列["not", "all", "heroes", "wear"]给出的情况下，(对于下一个token)模型预测"capes"具有最高的概率

为了针对整个序列获得下一个token预测， 我们可以简单的选择output[-1]中概率最大的那个token：

1
2
3
4
5
vocab = ["all", "not", "heroes", "the", "wear", ".", "capes"]
inputs = [1, 0, 2, 4] # "not" "all" "heroes" "wear"
output = gpt(inputs)
next_token_id = np.argmax(output[-1]) # next_token_id = 6
next_token = vocab[next_token_id] # next_token = "capes"

将具有最高概率的token作为我们的预测，叫做greedy decoding或者greedy sampling(贪心采样)。

在一个序列中预测下一个逻辑词(logical word)的任务被称之为语言建模。因此我们可以称GPT为语言模型。

生成一个单词是挺酷的（但也就那样了），但是要是生成整个句子、整篇文章呢？

生成文本

自回归

我们可以迭代地通过模型获取下一个token的预测，从而生成整个句子。在每次迭代中，我们将预测的token再添加回输入中去：

1
2
3
4
5
6
7
8
9
10
def generate(inputs, n_tokens_to_generate):
    for _ in range(n_tokens_to_generate): # 自回归的解码循环
        output = gpt(inputs) # 模型前向传递
        next_id = np.argmax(output[-1]) # 贪心采样
        inputs.append(int(next_id)) # 将预测添加回输入
    return inputs[len(inputs) - n_tokens_to_generate :]  # 只返回生成的ids

input_ids = [1, 0] # "not" "all"
output_ids = generate(input_ids, 3) # output_ids = [2, 4, 6]
output_tokens = [vocab[i] for i in output_ids] # "heroes" "wear" "capes"

这个过程是在预测未来的值（回归），并且将预测的值添加回输入中去（auto），这就是为什么你会看到GPT被描述为自回归模型。

采样

我们可以通过对概率分布进行采样来替代贪心采样，从而为我们的生成引入一些随机性（stochasticity）：

1
2
3
4
5
6
7
inputs = [1, 0, 2, 4] # "not" "all" "heroes" "wear"
output = gpt(inputs)
np.random.choice(np.arange(vocab_size), p=output[-1]) # capes
np.random.choice(np.arange(vocab_size), p=output[-1]) # hats
np.random.choice(np.arange(vocab_size), p=output[-1]) # capes
np.random.choice(np.arange(vocab_size), p=output[-1]) # capes
np.random.choice(np.arange(vocab_size), p=output[-1]) # pants

这样子，我们就可以基于同一个输入产生不同的输出句子啦。当我们结合更多的比如top-k，top-p和温度这样的技巧的时候，（这些技巧能够能更改采样的分布），我们输出的质量也会有很大的提高。这些技巧也引入了一些超参数，通过调整这些超参，我们可以获得不同的生成表现(behaviors)。比如提高温度超参，我们的模型就会更加冒进，从而变得更有“创造力”。

训练

我们与训练其它神经网络一样，针对特定的损失函数使用梯度下降训练GPT。对于GPT，我们使用语言建模任务的交叉熵损失：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def lm_loss(inputs: list[int], params) -> float:
    # the labels y are just the input shifted 1 to the left
    #
    # inputs = [not,     all,   heros,   wear,   capes]
    #      x = [not,     all,   heroes,  wear]
    #      y = [all,  heroes,     wear,  capes]
    #
    # of course, we don't have a label for inputs[-1], so we exclude it from x
    #
    # as such, for N inputs, we have N - 1 langauge modeling example pairs
    x, y = inputs[:-1], inputs[1:]

    # forward pass
    # all the predicted next token probability distributions at each position
    output = gpt(x, params)

    # cross entropy loss
    # we take the average over all N-1 examples
    loss = np.mean(-np.log(output[y]))

    return loss

def train(texts: list[list[str]], params) -> float:
    for text in texts:
        inputs = tokenizer.encode(text)
        loss = lm_loss(inputs, params)
        gradients = compute_gradients_via_backpropagation(loss, params)
        params = gradient_descent_update_step(gradients, params)
    return params

以上是一个极度简化的训练设置，但是它基本覆盖了重点。这里注意一下，我们的gpt函数签名中加入了params（为了简化，我们在上一节是把它去掉的）。在训练循环的每次迭代中：

  1. 我们为给定的输入文本示例计算语言建模损失
  2. 损失决定了我们的梯度，我们可以通过反向传播计算梯度
  3. 我们使用梯度来更新我们的模型参数，使得我们的损失能够最小化（梯度下降）

请注意，我们在这里并未使用明确的标注数据。取而代之的是，我们可以通过原始文本自身，产生大量的输入/标签对(input/label pairs)。这就是所谓的自监督学习。

自监督学习的范式，让我们能够海量扩充训练数据。我们只需要尽可能多的搞到大量的文本数据，然后将其丢入模型即可。比如，GPT-3就是基于来自互联网和书籍的3000亿token进行训练的：

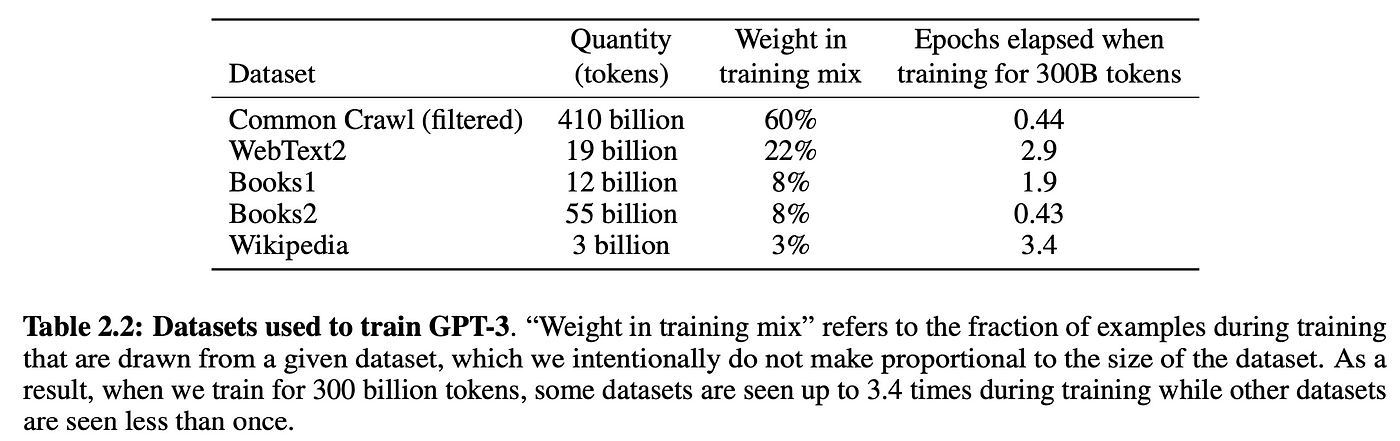
(table 2.2)

来自GPT-3论文的Table 2.2

当然，这里你就需要一个足够大的模型有能力去从这么大量的数据中学到内容，这就是为什么GPT-3模型拥有1750亿的参数，并且大概消耗了100万–1000万美元的计算费用进行训练[3]。

这个自监督训练的步骤称之为预训练，而我们可以重复使用预训练模型权重来训练下游任务上的特定模型，比如对文本进行分类（分类某条推文是有害的还是无害的）。预训练模型有时也被称为基础模型(foundation models)。

在下游任务上训练模型被称之为微调，由于模型权重已经预训练好了，已经能够理解语言了，那么我们需要做的就是针对特定的任务去微调这些权重。

译者注：听上去很简单是不是？那就快来入坑啊（doge）

这个所谓“在通用任务上预训练 + 特定任务上微调”的策略就称之为迁移学习。

提示（prompting）

本质上看，原始的GPT论文只是提供了用来迁移学习的transformer模型的预训练。文章显示，一个117M的GPT预训练模型，在针对下游任务的标注数据上微调之后，它能够在各种NLP(natural language processing)任务上达到最优性能。

直到GPT-2和GPT-3的论文出来，我们才意识到，一个GPT模型只要在足够多的数据上训练，只要模型拥有足够多的参数，那么不需要微调，模型本身就有能力执行各种任务。只要你对模型进行提示，运行自回归语言模型，然后你猜咋地？模型就神奇的返回给我们合适的响应了。这，就是所谓的in-context learning， 也就是说模型仅仅根据提示的内容，就能够执行各种任务了。In-context learning可以是zero shot, one shot, 或者是few shot的：

译者注：我们可以简单的认为，为了执行我们的自己的任务，zero shot表示我们直接拿着大模型就能用于我们的任务了；one shot表示我们需要提供给大模型关于我们特定任务的一个列子；few shot表示我们需要提供给大模型关于我们特定任务的几个例子；

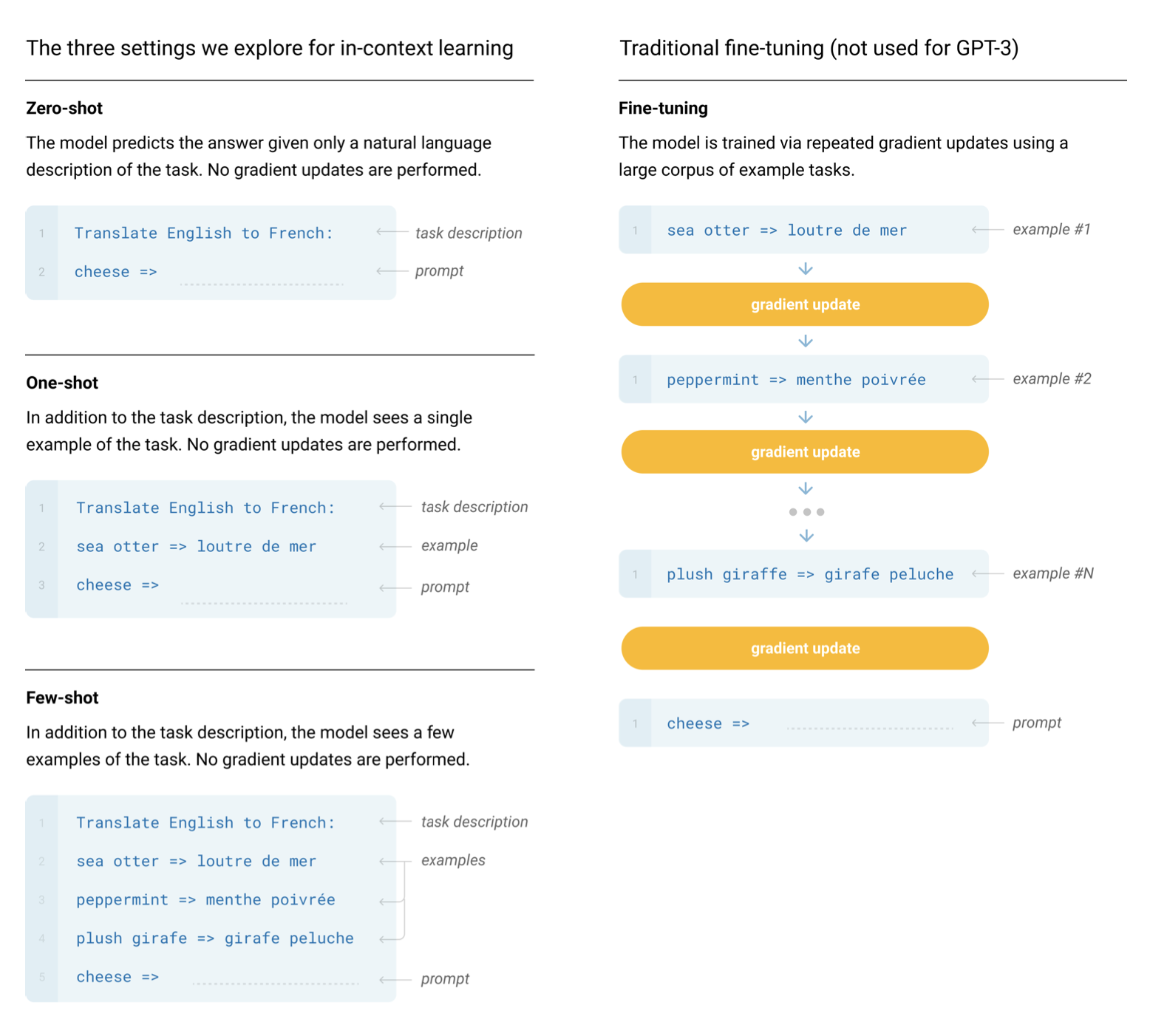
(fig 2.1)

来自GPT-3论文的图2.1

基于提示内容生成文本也被称之为条件生成，因为我们的模型是基于特定的输入（条件）进行生成的。

当然，GPT也不仅限于自然语言处理任务(NLP)。你可以将模型用于任何你想要的条件下。比如你可以将GPT变成一个聊天机器人(即：ChatGPT)，这里的条件就是你的对话历史。你也可以进一步条件化你的聊天机器人，通过提示词进行某种描述，限定其表现为某种行为（比如你可以提示：“你是个聊天机器人，请礼貌一点，请讲完整的句子，不要说有害的东西，等等”）。像这样条件化你的模型，你完全可以得到一个定制化私人助理机器人。但是这样的方式不一定很健壮，你仍然可以对你的模型进行越狱，然后让它表现失常。

译者注：原作者在这里主要讲了通过prompt进行条件控制，其实还有很多其它的条件化机器人的方法，有兴趣我可以另开一篇来单独细说

说完了这些，现在终于要开始实际实现了。

准备工作

首先将这个教程的仓库clone下来：

1
2
git clone https://github.com/jaymody/picoGPT
cd picoGPT

然后安装依赖：

1
pip install -r requirements.txt

注意：目前代码在Python 3.9.10下测试通过。

简单介绍一下每个文件：

  • encoder.py包含了OpenAI的BPE分词器的代码，这是直接从gpt-2仓库拿过来的
  • utils.py：包含下载并加载GPT-2模型的权重，分词器和超参数
  • gpt2.py：包含了实际GPT模型以及生成的代码，这个代码可以作为python脚本直接运行
  • gpt2_pico.py：和gpt2.py一样，但是行数变少了。你问为什么？你猜

在这里，我们将从0-1复现gpt2.py，所以请先将这个文件删掉吧，我们重新建立一个新的gpt2.py文件，然后从头写起：

1
2
rm gpt2.py
touch gpt2.py

首先，将下面的代码粘贴到gpt2.py里：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import numpy as np


def gpt2(inputs, wte, wpe, blocks, ln_f, n_head):
    pass # TODO: implement this


def generate(inputs, params, n_head, n_tokens_to_generate):
    from tqdm import tqdm

    for _ in tqdm(range(n_tokens_to_generate), "generating"):  # auto-regressive decode loop
        logits = gpt2(inputs, **params, n_head=n_head)  # model forward pass
        next_id = np.argmax(logits[-1])  # greedy sampling
        inputs.append(int(next_id))  # append prediction to input

    return inputs[len(inputs) - n_tokens_to_generate :]  # only return generated ids


def main(prompt: str, n_tokens_to_generate: int = 40, model_size: str = "124M", models_dir: str = "models"):
    from utils import load_encoder_hparams_and_params

    # load encoder, hparams, and params from the released open-ai gpt-2 files
    encoder, hparams, params = load_encoder_hparams_and_params(model_size, models_dir)

    # encode the input string using the BPE tokenizer
    input_ids = encoder.encode(prompt)

    # make sure we are not surpassing the max sequence length of our model
    assert len(input_ids) + n_tokens_to_generate < hparams["n_ctx"]

    # generate output ids
    output_ids = generate(input_ids, params, hparams["n_head"], n_tokens_to_generate)

    # decode the ids back into a string
    output_text = encoder.decode(output_ids)

    return output_text


if __name__ == "__main__":
    import fire

    fire.Fire(main)

我们将分为四部分进行拆解：

  1. gpt2函数是我们将要实现的实际GPT代码。你会注意到函数签名中除了inputs，还有其它的参数：

    • wte, wpe, blocks, ln_f这些都是我们模型的参数
    • n_head是前向计算过程中需要的超参

  2. generate函数是我们之前看到的自回归解码算法。为了简洁，我们使用贪心采样算法。tqdm是一个进度条库，它可以帮助我们随着每次生成一个token，可视化地观察解码过程。

  3. main函数主要处理：

    • 1.加载分词器(encoder)， 模型权重（params）， 超参（hparams）
    • 2.使用分词器将输入提示词编码为token ID
    • 3.调用生成函数
    • 4.将输出ID解码为字符串

  4. fire.Fire(main)将我们的源文件转成一个命令行应用，然后就可以像这样运行我们的代码了：python gpt2.py "some prompt here"

我们先在notebook或者python交互界面下看看encoder, hparams, params，运行：

1
2
from utils import load_encoder_hparams_and_params
encoder, hparams, params = load_encoder_hparams_and_params("124M", "models")

上述代码将下载必要的模型及分词器文件至models/124M，并且加载encoder,hparams,params。

编码器

我们的encoder使用的是GPT-2中使用的BPE分词器：

1
2
3
4
5
6
>>> ids = encoder.encode("Not all heroes wear capes.")
>>> ids
[3673, 477, 10281, 5806, 1451, 274, 13]

>>> encoder.decode(ids)
"Not all heroes wear capes."

使用分词器的词汇表(存储于encoder.decoder)，我们可以看看实际的token到底长啥样：

1
2
>>> [encoder.decoder[i] for i in ids]
['Not', 'Ġall', 'Ġheroes', 'Ġwear', 'Ġcap', 'es', '.']

注意，有的时候我们的token是单词（比如：Not），有的时候虽然也是单词，但是可能会有一个空格在它前面（比如Ġall, Ġ代表一个空格），有时候是一个单词的一部分（比如：capes被分隔为Ġcap和es），还有可能它就是标点符号（比如：.）。

BPE的一个好处是它可以编码任意字符串。如果遇到了某些没有在词汇表里显示的字符串，那么BPE就会将其分割为它能够理解的子串：

1
2
>>> [encoder.decoder[i] for i in encoder.encode("zjqfl")]
['z', 'j', 'q', 'fl']

我们还可以检查一下词汇表的大小：

1
2
>>> len(encoder.decoder)
50257

词汇表以及决定字符串如何分解的字节对组合（byte-pair merges），是通过训练分词器获得的。当我们加载分词器，就会从一些文件加载已经训练好的词汇表和字节对组合，这些文件在我们运行load_encoder_hparams_and_params的时候，随着模型文件被一起下载了。你可以查看models/124M/encoder.json(词汇表)和models/124M/vocab.bpe(字节对组合)。

超参数

hparams是一个字典，这个字典包含着我们模型的超参：

1
2
3
4
5
6
7
8
>>> hparams
{
  "n_vocab": 50257, # number of tokens in our vocabulary
  "n_ctx": 1024, # maximum possible sequence length of the input
  "n_embd": 768, # embedding dimension (determines the "width" of the network)
  "n_head": 12, # number of attention heads (n_embd must be divisible by n_head)
  "n_layer": 12 # number of layers (determines the "depth" of the network)
}

我们将在代码的注释中使用这些符号来表示各种的大小维度等等。我们还会使用n_seq来表示输入序列的长度(即：n_seq = len(inputs))。

参数

params是一个嵌套的json字典，该字典具有模型训练好的权重。json的叶子节点是NumPy数组。如果我们打印params， 用他们的形状去表示数组，我们可以得到：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
>>> import numpy as np
>>> def shape_tree(d):
>>>     if isinstance(d, np.ndarray):
>>>         return list(d.shape)
>>>     elif isinstance(d, list):
>>>         return [shape_tree(v) for v in d]
>>>     elif isinstance(d, dict):
>>>         return {k: shape_tree(v) for k, v in d.items()}
>>>     else:
>>>         ValueError("uh oh")
>>>
>>> print(shape_tree(params))
{
    "wpe": [1024, 768],
    "wte": [50257, 768],
    "ln_f": {"b": [768], "g": [768]},
    "blocks": [
        {
            "attn": {
                "c_attn": {"b": [2304], "w": [768, 2304]},
                "c_proj": {"b": [768], "w": [768, 768]},
            },
            "ln_1": {"b": [768], "g": [768]},
            "ln_2": {"b": [768], "g": [768]},
            "mlp": {
                "c_fc": {"b": [3072], "w": [768, 3072]},
                "c_proj": {"b": [768], "w": [3072, 768]},
            },
        },
        ... # repeat for n_layers
    ]
}

这些是从原始的OpenAI TensorFlow checkpoint加载的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
>>> import tensorflow as tf
>>> tf_ckpt_path = tf.train.latest_checkpoint("models/124M")
>>> for name, _ in tf.train.list_variables(tf_ckpt_path):
>>>     arr = tf.train.load_variable(tf_ckpt_path, name).squeeze()
>>>     print(f"{name}: {arr.shape}")
model/h0/attn/c_attn/b: (2304,)
model/h0/attn/c_attn/w: (768, 2304)
model/h0/attn/c_proj/b: (768,)
model/h0/attn/c_proj/w: (768, 768)
model/h0/ln_1/b: (768,)
model/h0/ln_1/g: (768,)
model/h0/ln_2/b: (768,)
model/h0/ln_2/g: (768,)
model/h0/mlp/c_fc/b: (3072,)
model/h0/mlp/c_fc/w: (768, 3072)
model/h0/mlp/c_proj/b: (768,)
model/h0/mlp/c_proj/w: (3072, 768)
model/h1/attn/c_attn/b: (2304,)
model/h1/attn/c_attn/w: (768, 2304)
...
model/h9/mlp/c_proj/b: (768,)
model/h9/mlp/c_proj/w: (3072, 768)
model/ln_f/b: (768,)
model/ln_f/g: (768,)
model/wpe: (1024, 768)
model/wte: (50257, 768)

下述代码将上面的tensorflow变量转换为params字典。

为了对比，这里显示了params的形状，但是数字被hparams替代：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
{
    "wpe": [n_ctx, n_embd],
    "wte": [n_vocab, n_embd],
    "ln_f": {"b": [n_embd], "g": [n_embd]},
    "blocks": [
        {
            "attn": {
                "c_attn": {"b": [3*n_embd], "w": [n_embd, 3*n_embd]},
                "c_proj": {"b": [n_embd], "w": [n_embd, n_embd]},
            },
            "ln_1": {"b": [n_embd], "g": [n_embd]},
            "ln_2": {"b": [n_embd], "g": [n_embd]},
            "mlp": {
                "c_fc": {"b": [4*n_embd], "w": [n_embd, 4*n_embd]},
                "c_proj": {"b": [n_embd], "w": [4*n_embd, n_embd]},
            },
        },
        ... # repeat for n_layers
    ]
}

在实现GPT的过程中，你可能会需要参考这个字典来确认权重的形状。为了一致性，我们将会使代码中的变量名和字典的键值保持对齐。

基础层

在进入实际GPT架构前的最后一件事，让我们来手搓几个基础的神经网络层吧，这些基础层可不只是针对GPT的，它们在各种情况下都很有用。

GELU

GPT-2的非线性（激活函数）选择是GELU（高斯误差线性单元），这是一种类似ReLU的激活函数：

来自GELU论文的图1

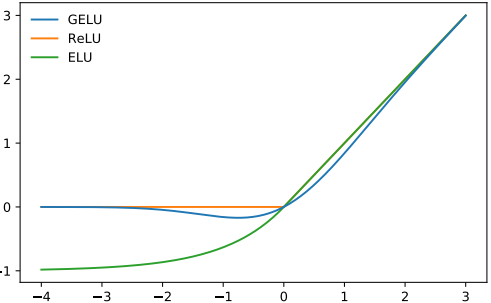
它的函数函数如下：

1
2
def gelu(x):
    return 0.5 * x * (1 + np.tanh(np.sqrt(2 / np.pi) * (x + 0.044715 * x**3)))

和ReLU类似，GELU也对输入进行逐元素操作：

1
2
3
4

>>> gelu(np.array([[1, 2], [-2, 0.5]]))
array([[ 0.84119,  1.9546 ],
       [-0.0454 ,  0.34571]])

Softmax

下面是最经典的softmax:

$$\text{softmax}(x)_i = \frac{e^{x_i}}{\sum_j e^{x_j}}$$

1
2
3
def softmax(x):
    exp_x = np.exp(x - np.max(x, axis=-1, keepdims=True))
    return exp_x / np.sum(exp_x, axis=-1, keepdims=True)

这里我们使用了max(x)技巧来保持数值稳定性。

softmax用来将一组实数（$-\infty$至$\infty$之间）转换为概率（$0$至$1$之间，其求和为1）。我们将softmax作用于输入的最末轴上。

1
2
3
4
5
6
>>> x = softmax(np.array([[2, 100], [-5, 0]]))
>>> x
array([[0.00034, 0.99966],
       [0.26894, 0.73106]])
>>> x.sum(axis=-1)
array([1., 1.])

层归一化

层归一化将数值标准化为均值为0方差为1的值：

$$\text{LayerNorm}(x) = \gamma \cdot \frac{x - \mu}{\sqrt{\sigma^2}} + \beta$$

其中$\mu$是$x$的均值，$\sigma^2$为$x$的方差，$\gamma$和$\beta$为可学习的参数。

1
2
3
4
5
def layer_norm(x, g, b, eps: float = 1e-5):
    mean = np.mean(x, axis=-1, keepdims=True)
    variance = np.var(x, axis=-1, keepdims=True)
    x = (x - mean) / np.sqrt(variance + eps)  # normalize x to have mean=0 and var=1 over last axis
    return g * x + b  # scale and offset with gamma/beta params

层归一化确保每层的输入总是在一个一致的范围里，而这将为训练过程的加速和稳定提供支持。与批归一化类似，归一化之后的输出通过两个可学习参数$\gamma$和$\beta$进行缩放和偏移。分母中的小epsilon项用来避免计算中的分母为零错误。

我们在transformer中用层归一化来替换批归一化的原因有很多。各种不同归一化技巧的不同点在这个博客中进行了精彩的总结。

我们对输入的最末轴进行层归一化：

1
2
3
4
5
6
7
8
9
>>> x = np.array([[2, 2, 3], [-5, 0, 1]])
>>> x = layer_norm(x, g=np.ones(x.shape[-1]), b=np.zeros(x.shape[-1]))
>>> x
array([[-0.70709, -0.70709,  1.41418],
       [-1.397  ,  0.508  ,  0.889  ]])
>>> x.var(axis=-1)
array([0.99996, 1.     ]) # floating point shenanigans
>>> x.mean(axis=-1)
array([-0., -0.])

线性（变换）

这里是标准的矩阵乘法+偏置：

1
2
def linear(x, w, b):  # [m, in], [in, out], [out] -> [m, out]
    return x @ w + b

线性层也通常被认为是投影操作（因为它们将一个向量空间投影到另一个向量空间）。

1
2
3
4
5
6
7
8

>>> x = np.random.normal(size=(64, 784)) # input dim = 784, batch/sequence dim = 64
>>> w = np.random.normal(size=(784, 10)) # output dim = 10
>>> b = np.random.normal(size=(10,))
>>> x.shape # shape before linear projection
(64, 784)
>>> linear(x, w, b).shape # shape after linear projection
(64, 10)

GPT架构

GPT的架构是基于transformer的：

来自Attention is All You Need论文的图1

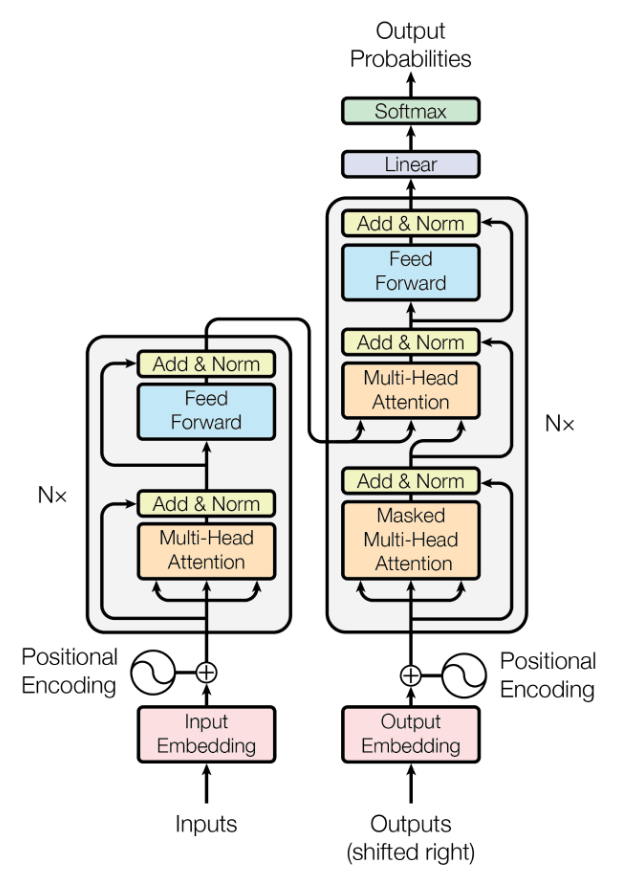
但它仅仅使用了解码器层（图中的右边部分）：

  GPT架构

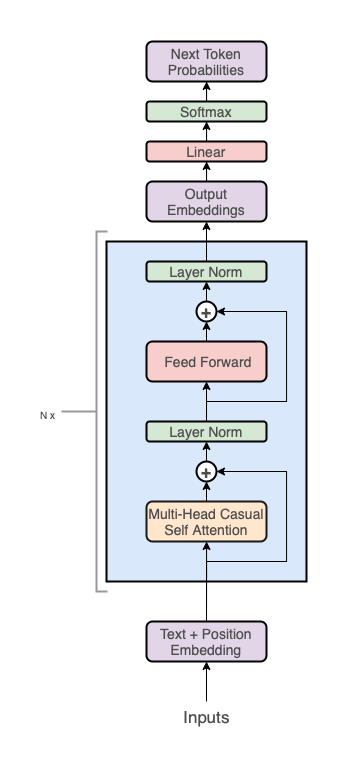
注意，因为我们已经搞定了编码器，所以中间的”cross-attention”层也被移除了。

从宏观的角度来看，GPT架构有三个部分组成：

  • 文本 + 位置嵌入(positional embeddings)
  • 基于transformer的解码器层(decoder stack)
  • 投影为词汇表(projection to vocab)的步骤

代码层面的话，就像这样：

1
2
3
4
5
6
7
8
9
10
11
def gpt2(inputs, wte, wpe, blocks, ln_f, n_head):  # [n_seq] -> [n_seq, n_vocab]
    # token + positional embeddings
    x = wte[inputs] + wpe[range(len(inputs))]  # [n_seq] -> [n_seq, n_embd]

    # forward pass through n_layer transformer blocks
    for block in blocks:
        x = transformer_block(x, **block, n_head=n_head)  # [n_seq, n_embd] -> [n_seq, n_embd]

    # projection to vocab
    x = layer_norm(x, **ln_f)  # [n_seq, n_embd] -> [n_seq, n_embd]
    return x @ wte.T  # [n_seq, n_embd] -> [n_seq, n_vocab]

现在我们将上面三个部分做更细致的拆解。

嵌入层

Token 嵌入

对于神经网络而言，token ID本身并不是一个好的表示。第一，token ID的相对大小会传递错误的信息（比如，在我们的词汇表中，如果Apple = 5，Table=10，那就意味着2 * Table = Apple？显然不对）。其二，单个的数也没有足够的维度喂给神经网络。

译者注：对于第二点补充一句，也就是说单个的数字包含的特征信息不够丰富

为了解决这些限制，我们将利用词向量，即通过一个学习到的嵌入矩阵：

1
wte[inputs] # [n_seq] -> [n_seq, n_embd]

还记得吗？wte是一个[n_vocab, n_emdb]的矩阵。这就像一个查找表，矩阵中的第$i$行对应我们的词汇表中的第$i$个token的向量表示（学出来的）。wte[inputs]使用了integer array indexing来检索我们输入中每个token所对应的向量。

就像神经网络中的其他参数，wte是可学习的。也就是说，在训练开始的时候它是随机初始化的，然后随着训练的进行，通过梯度下降不断更新。

位置嵌入（Positional Embeddings）

单纯的transformer架构的一个古怪地方在于它并不考虑位置。当我们随机打乱输入位置顺序的时候，输出可以保持不变（输入的顺序对输出并未产生影响）。

可是词的顺序当然是语言中重要的部分啊，因此我们需要使用某些方式将位置信息编码进我们的输入。为了这个目标，我们可以使用另一个学习到的嵌入矩阵：

1
wpe[range(len(inputs))] # [n_seq] -> [n_seq, n_embd]

wpe是一个[n_ctx, n_emdb]矩阵。矩阵的第$i$行包含一个编码输入中第$i$个位置信息的向量。与wte类似，这个矩阵也是通过梯度下降来学习到的。

需要注意的是，这将限制模型的最大序列长度为n_ctx[4]。也就是说必须满足len(inputs) <= n_ctx。

组合

现在我们可以将token嵌入与位置嵌入联合为一个组合嵌入，这个嵌入将token信息和位置信息都编码进来了。

1
2
3
4
5
# token + positional embeddings
x = wte[inputs] + wpe[range(len(inputs))]  # [n_seq] -> [n_seq, n_embd]

# x[i] represents the word embedding for the ith word + the positional
# embedding for the ith position

解码层

这就是神奇发生的地方了，也是深度学习中“深度“的来源。我们将刚才的嵌入通过一连串的n_layertransformer解码器模块。

1
2
3
# forward pass through n_layer transformer blocks
for block in blocks:
    x = transformer_block(x, **block, n_head=n_head)  # [n_seq, n_embd] -> [n_seq, n_embd]

一方面，堆叠更多的层让我们可以控制到底我们的网络有多“深”。以GPT-3为例，其高达96层。另一方面，选择一个更大的n_embd值，让我们可以控制网络有多“宽”（还是以GPT-3为例，它使用的嵌入大小为12288）。

投影为词汇表(projection to vocab)

在最后的步骤中，我们将transformer最后一个结构块的输入投影为字符表的一个概率分布：

1
2
3
4

# projection to vocab
x = layer_norm(x, **ln_f)  # [n_seq, n_embd] -> [n_seq, n_embd]
return x @ wte.T  # [n_seq, n_embd] -> [n_seq, n_vocab]

这里有一些需要注意的点：

  1. 在进行投影操作之前，我们先将x通过最后的层归一化层。这是GPT-2架构所特有的（并没有出现在GPT原始论文和Transformer论文中）。
  2. 我们复用了嵌入矩阵wte进行投影操作。其它的GPT实现当然可以选择使用另外学习到的权重矩阵进行投影，但是权重矩阵共享具有以下一些优势：
    • 你可以节省一些参数（虽然对于GPT-3这样的体量，这个节省基本可以忽略）
    • 考虑到这个矩阵作用于转换到词与来自于词的两种转换，理论上，相对于分别使用两个矩阵来做这件事，使用同一个矩阵将学到更为丰富的表征。
  3. 在最后，我们并未使用softmax，因此我们的输出是logits而不是0-1之间的概率。这样做的理由是：
    • softmax是单调的，因此对于贪心采样而言，np.argmax(logits)和np.argmax(softmax(logits))是等价的，因此使用softmax就变得多此一举。
    • softmax是不可逆的，这意味着我们总是可以通过softmax将logits变为probabilities，但不能从probabilities变为softmax，为了让灵活性最大，我们选择直接输出logits。
    • 数值稳定性的考量。比如计算交叉熵损失的时候，相对于log_softmax(logits)，log(softmax(logits))的数值稳定性就差。

投影为词汇表的过程有时候也被称之为语言建模头（language modeling head）。这里的“头”是什么意思呢？你的GPT一旦被预训练完毕，那么你可以通过更换其他投影操作的语言建模头，比如你可以将其更换为分类头，从而在一些分类任务上微调你的模型（让其完成分类任务）。因此你的模型可以拥有多种头，感觉有点像hydra。

译者注：hydra是希腊神话中的九头蛇，感受一下

好了，以上就是GPT架构的宏观介绍。那么现在我们再来看看解码器模块的细节。

解码器模块

transformer解码器模块由两个子层组成：

  1. 多头因果自注意力（Multi-head causal self attention）
  2. 逐位置前馈神经网络（Position-wise feed forward neural network）
1
2
3
4
5
6
7
8
def transformer_block(x, mlp, attn, ln_1, ln_2, n_head):  # [n_seq, n_embd] -> [n_seq, n_embd]
    # multi-head causal self attention
    x = x + mha(layer_norm(x, **ln_1), **attn, n_head=n_head)  # [n_seq, n_embd] -> [n_seq, n_embd]

    # position-wise feed forward network
    x = x + ffn(layer_norm(x, **ln_2), **mlp)  # [n_seq, n_embd] -> [n_seq, n_embd]

    return x

每个子层都在输入上使用了层归一化，也使用了残差连接（即将子层的输入直接连接到子层的输出）。

先讲几条注意点：

  1. 多头因果自注意力机制便于输入之间的通信。在网络的其它地方，模型是不允许输入相互“看到”彼此的。嵌入层、逐位置前馈网络、层归一化以及投影到词汇表的操作，都是逐位置对我们的输入进行的。建模输入之间的关系完全由注意力机制来处理。

  2. 逐位置前馈神经网络只是一个常规的两层全连接神经网络。它只是为我们的模型增加一些可学习的参数，以促进学习过程。

  3. 在原始的transformer论文中，层归一化被放置在输出层layer_norm(x + sublayer(x))上，而我们在这里为了匹配GPT-2，将层归一化放置在输入x + sublayer(layer_norm(x))上。这被称为预归一化，并且已被证明在改善transformer的性能方面非常重要。

  4. 残差连接（由于ResNet而广为人知）这这里有几个不同的目的：

    • 1.使得深度神经网络（即层数非常多的神经网络）更容易进行优化。其思想是为梯度提供“捷径”，使得梯度更容易地回传到网络的初始的层，从而更容易进行优化。
    • 2.如果没有残差连接的话，加深模型层数会导致性能下降（可能是因为梯度很难在没有损失信息的情况下回传到整个深层网络中）。残差连接似乎可以为更深层的网络提供一些精度提升。
    • 3.可以帮助解决梯度消失/爆炸的问题。

现在我们再深入讨论一下这两个子层。

逐位置前馈网络

逐位置前馈网络（Position-wise Feed Forward Network）是一个简单的两层的多层感知器：

1
2
3
4
5
6
7
8
def ffn(x, c_fc, c_proj):  # [n_seq, n_embd] -> [n_seq, n_embd]
    # project up
    a = gelu(linear(x, **c_fc))  # [n_seq, n_embd] -> [n_seq, 4*n_embd]

    # project back down
    x = linear(a, **c_proj)  # [n_seq, 4*n_embd] -> [n_seq, n_embd]

    return x

这里没有什么特别的技巧，我们只是将n_embd投影到一个更高的维度4*n_embd，然后再将其投影回n_embd[5]。

回忆一下我们的params字典，我们的mlp参数如下：

1
2
3
4
"mlp": {
    "c_fc": {"b": [4*n_embd], "w": [n_embd, 4*n_embd]},
    "c_proj": {"b": [n_embd], "w": [4*n_embd, n_embd]},
}

多头因果自注意力

这一层可能是理解transformer最困难的部分。因此我们通过分别解释“多头因果自注意力”的每个词，一步步理解“多头因果自注意力”：

  1. 注意力（Attention）
  2. 自身（Self）
  3. 因果（Causal）
  4. 多头（Multi-Head）

注意力

我还有另一篇关于这个话题的博客文章，那篇博客中，我从头开始推导了原始transformer论文中提出的缩放点积方程：

$$\text{attention}(Q, K, V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V$$

因此在这篇文章中，我将跳过关于注意力的解释。您也可以参考 Lilian Weng 的 Attention? Attention!和Jay Alammar的The Illustrated Transformer，这两篇也对注意力机制做了极好的解释。

我们现在只要去适配我博客文章中的注意力实现：

1
2
def attention(q, k, v):  # [n_q, d_k], [n_k, d_k], [n_k, d_v] -> [n_q, d_v]
    return softmax(q @ k.T / np.sqrt(q.shape[-1])) @ v

自身(Self)

当q, k和v来自同一来源时，我们就是在执行自注意力（即让我们的输入序列自我关注）：

1
2
def self_attention(x): # [n_seq, n_embd] -> [n_seq, n_embd]
    return attention(q=x, k=x, v=x)

例如，如果我们的输入是“Jay went to the store, he bought 10 apples.”，我们让单词“he”关注所有其它单词，包括“Jay”，这意味着模型可以学习到“he”指的是“Jay”。

译者注：注意这里是英文的文本

我们可以通过为q、k、v和注意力输出引入投影来增强自注意力：

1
2
3
4
5
6
7
8
9
10
11
12
13
def self_attention(x, w_k, w_q, w_v, w_proj): # [n_seq, n_embd] -> [n_seq, n_embd]
    # qkv projections
    q = x @ w_k # [n_seq, n_embd] @ [n_embd, n_embd] -> [n_seq, n_embd]
    k = x @ w_q # [n_seq, n_embd] @ [n_embd, n_embd] -> [n_seq, n_embd]
    v = x @ w_v # [n_seq, n_embd] @ [n_embd, n_embd] -> [n_seq, n_embd]

    # perform self attention
    x = attention(q, k, v) # [n_seq, n_embd] -> [n_seq, n_embd]

    # out projection
    x = x @ w_proj # [n_seq, n_embd] @ [n_embd, n_embd] -> [n_seq, n_embd]

    return x

这使得我们的模型为q, k, v学到一个最好的映射，以帮助注意力区分输入之间的关系。

如果我们将w_q、w_k和w_v组合成一个单独的矩阵w_fc，执行投影操作，然后拆分结果，我们就可以将矩阵乘法的数量从4个减少到2个：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def self_attention(x, w_fc, w_proj): # [n_seq, n_embd] -> [n_seq, n_embd]
    # qkv projections
    x = x @ w_fc # [n_seq, n_embd] @ [n_embd, 3*n_embd] -> [n_seq, 3*n_embd]

    # split into qkv
    q, k, v = np.split(x, 3, axis=-1) # [n_seq, 3*n_embd] -> 3 of [n_seq, n_embd]

    # perform self attention
    x = attention(q, k, v) # [n_seq, n_embd] -> [n_seq, n_embd]

    # out projection
    x = x @ w_proj # [n_seq, n_embd] @ [n_embd, n_embd] = [n_seq, n_embd]

    return x

这样会更加高效，因为现代加速器（如GPU）可以更好地利用一个大的矩阵乘法，而不是顺序执行3个独立的小矩阵乘法。

最后，我们添加偏置向量以匹配GPT-2的实现，然后使用我们的linear函数，并将参数重命名以匹配我们的params字典：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def self_attention(x, c_attn, c_proj): # [n_seq, n_embd] -> [n_seq, n_embd]
    # qkv projections
    x = linear(x, **c_attn) # [n_seq, n_embd] -> [n_seq, 3*n_embd]

    # split into qkv
    q, k, v = np.split(x, 3, axis=-1) # [n_seq, 3*n_embd] -> 3 of [n_seq, n_embd]

    # perform self attention
    x = attention(q, k, v) # [n_seq, n_embd] -> [n_seq, n_embd]

    # out projection
    x = linear(x, **c_proj) # [n_seq, n_embd] @ [n_embd, n_embd] = [n_seq, n_embd]

    return x

回忆一下，从我们的params字典中可知，attn参数类似：

1
2
3
4
"attn": {
    "c_attn": {"b": [3*n_embd], "w": [n_embd, 3*n_embd]},
    "c_proj": {"b": [n_embd], "w": [n_embd, n_embd]},
},

因果

我们当前的自注意力设置存在一个问题，就是我们的输入能够“看到”未来的信息！比如，如果我们的输入是[“not”, “all”, “heroes”, “wear”, “capes”]，在自注意力中，“wear”可以看到“capes”。这意味着“wear”的输出概率将会受到偏差，因为模型已经知道正确的答案是“capes”。这是不好的，因为我们的模型会从中学习到，输入$i$的正确答案可以从输入$i+1$中获取。

为了防止这种情况发生，我们需要修改注意力矩阵，以隐藏或屏蔽我们的输入，使其无法看到未来的信息。例如，假设我们的注意力矩阵如下所示：

1
2
3
4
5
6
        not    all    heroes wear   capes
   not 0.116  0.159  0.055  0.226  0.443
   all 0.180  0.397  0.142  0.106  0.175
heroes 0.156  0.453  0.028  0.129  0.234
  wear 0.499  0.055  0.133  0.017  0.295
 capes 0.089  0.290  0.240  0.228  0.153

这里每一行对应一个查询(query)，每一列对应一个键值(key)。在这个例子中，查看 “wear” 对应的行，可以看到它在最后一列以0.295的权重与 “capes” 相关。为了防止这种情况发生，我们要将这项设为0.0:

1
2
3
4
5
6
        not    all    heroes wear   capes
   not 0.116  0.159  0.055  0.226  0.443
   all 0.180  0.397  0.142  0.106  0.175
heroes 0.156  0.453  0.028  0.129  0.234
  wear 0.499  0.055  0.133  0.017  0.
 capes 0.089  0.290  0.240  0.228  0.153

通常，为了防止输入中的所有查询看到未来信息，我们将所有满足$j > i$的位置$i$, $j$都设置为0：

1
2
3
4
5
6
         not    all    heroes wear   capes
   not 0.116  0.     0.     0.     0.
   all 0.180  0.397  0.     0.     0.
heroes 0.156  0.453  0.028  0.     0.
  wear 0.499  0.055  0.133  0.017  0.
 capes 0.089  0.290  0.240  0.228  0.153

我们将这称为掩码(masking)。掩码方法的一个问题是我们的行不再加起来为1（因为我们在使用softmax后才将它们设为0）。为了确保我们的行仍然加起来为1，我们需要在使用softmax之前先修改注意力矩阵。

这可以通过在softmax之前将需要被掩码的条目设置为$-\infty$来实现[6]：

1
2
def attention(q, k, v, mask):  # [n_q, d_k], [n_k, d_k], [n_k, d_v], [n_q, n_k] -> [n_q, d_v]
    return softmax(q @ k.T / np.sqrt(q.shape[-1]) + mask) @ v

其中mask表示矩阵（n_seq=5）：

1
2
3
4
5
0 -1e10 -1e10 -1e10 -1e10
0   0   -1e10 -1e10 -1e10
0   0     0   -1e10 -1e10
0   0     0     0   -1e10
0   0     0     0     0

我们用-1e10替换-np.inf， 因为-np.inf会导致nans错误。

添加mask到我们的注意力矩阵中，而不是明确设置值为-1e10，是因为在实际操作中，任何数加上-inf还是-inf。

我们可以在NumPy中通过(1 - np.tri(n_seq)) * -1e10来计算mask矩阵。

将以上这些组合起来，我们得到：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def attention(q, k, v, mask):  # [n_q, d_k], [n_k, d_k], [n_k, d_v], [n_q, n_k] -> [n_q, d_v]
    return softmax(q @ k.T / np.sqrt(q.shape[-1]) + mask) @ v

def causal_self_attention(x, c_attn, c_proj): # [n_seq, n_embd] -> [n_seq, n_embd]
    # qkv projections
    x = linear(x, **c_attn) # [n_seq, n_embd] -> [n_seq, 3*n_embd]

    # split into qkv
    q, k, v = np.split(x, 3, axis=-1) # [n_seq, 3*n_embd] -> 3 of [n_seq, n_embd]

    # causal mask to hide future inputs from being attended to
    causal_mask = (1 - np.tri(x.shape[0]), dtype=x.dtype) * -1e10  # [n_seq, n_seq]

    # perform causal self attention
    x = attention(q, k, v, causal_mask) # [n_seq, n_embd] -> [n_seq, n_embd]

    # out projection
    x = linear(x, **c_proj) # [n_seq, n_embd] @ [n_embd, n_embd] = [n_seq, n_embd]

    return x

多头

我们可以进一步改进我们的实现，通过进行n_head个独立的注意力计算，将我们的查询（queries），键（keys）和值（values）拆分到多个头（heads）里去：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def mha(x, c_attn, c_proj, n_head):  # [n_seq, n_embd] -> [n_seq, n_embd]
    # qkv projection
    x = linear(x, **c_attn)  # [n_seq, n_embd] -> [n_seq, 3*n_embd]

    # split into qkv
    qkv = np.split(x, 3, axis=-1)  # [n_seq, 3*n_embd] -> [3, n_seq, n_embd]

    # split into heads
    qkv_heads = list(map(lambda x: np.split(x, n_head, axis=-1), qkv))  # [3, n_seq, n_embd] -> [3, n_head, n_seq, n_embd/n_head]

    # causal mask to hide future inputs from being attended to
    causal_mask = (1 - np.tri(x.shape[0]), dtype=x.dtype) * -1e10  # [n_seq, n_seq]

    # perform attention over each head
    out_heads = [attention(q, k, v, causal_mask) for q, k, v in zip(*qkv_heads)]  # [3, n_head, n_seq, n_embd/n_head] -> [n_head, n_seq, n_embd/n_head]

    # merge heads
    x = np.hstack(out_heads)  # [n_head, n_seq, n_embd/n_head] -> [n_seq, n_embd]

    # out projection
    x = linear(x, **c_proj)  # [n_seq, n_embd] -> [n_seq, n_embd]

    return x

这里添加了三步:

  1. 拆分q， k， v到n_head个头：
1
2
# split into heads
qkv_heads = list(map(lambda x: np.split(x, n_head, axis=-1), qkv))  # [3, n_seq, n_embd] -> [n_head, 3, n_seq, n_embd/n_head]
  1. 为每个头计算注意力：
1
2
# perform attention over each head
out_heads = [attention(q, k, v) for q, k, v in zip(*qkv_heads)]  # [n_head, 3, n_seq, n_embd/n_head] -> [n_head, n_seq, n_embd/n_head]
  1. 合并每个头的输出：
1
2
# merge heads
x = np.hstack(out_heads)  # [n_head, n_seq, n_embd/n_head] -> [n_seq, n_embd]

注意，这样可以将每个注意力计算的维度从n_embd减少到n_embd/n_head。这是一个权衡。对于缩减了的维度，我们的模型在通过注意力建模关系时获得了额外的子空间。例如，也许一个注意力头负责将代词与代词所指的人联系起来；也许另一个注意力头负责通过句号将句子分组；另一个则可能只是识别哪些单词是实体，哪些不是。虽然这可能也只是另一个神经网络黑盒而已。

译者注：哪里都有隐空间(doge)

我们编写的代码按顺序循环执行每个头的注意力计算（每次一个），当然这并不是很高效。在实践中，你会希望并行处理这些计算。当然在本文中考虑到简洁性，我们将保持这种顺序执行。

好啦，有了以上这些，我们终于完成了GPT的实现！现在要做的就是将它们组合起来并运行代码。

将所有代码组合起来

将所有代码组合起来，我们就得到了gpt2.py，总共的代码只有120行（如果你移除注释、空格之类的，那就只有60行）。

我们可以通过以下代码测试：

1
2
3
python gpt2.py \
    "Alan Turing theorized that computers would one day become" \
    --n_tokens_to_generate 8

其输出是：

1
the most powerful machines on the planet.

成功运行！！！

我们可以使用以下Dockerfile验证我们的实现与OpenAI的官方GPT-2仓库产生相同的结果（注意：这在M1 Macbooks上无法运行，这里涉及到TensorFlow的支持问题。还有一个警告是：这会下载所有4个GPT-2模型，而这意味着大量GB规模的文件需要被下载）：

1
2
3
4
docker build -t "openai-gpt-2" "https://gist.githubusercontent.com/jaymody/9054ca64eeea7fad1b58a185696bb518/raw/Dockerfile"
docker run -dt "openai-gpt-2" --name "openai-gpt-2-app"
docker exec -it "openai-gpt-2-app" /bin/bash -c 'python3 src/interactive_conditional_samples.py --length 8 --model_type 124M --top_k 1'
# paste "Alan Turing theorized that computers would one day become" when prompted

这里应该会给出完全相同的结果：

1
the most powerful machines on the planet.

下一步呢？

这个实现虽然不错，但还缺少很多额外的功能：

GPU/TPU 支持

将NumPy替换为JAX：

1
import jax.numpy as np

搞定！现在你可以在GPU甚至是TPU上使用这个代码了！前提是你正确地安装了JAX。

译者注：JAX是个好东西：）

反向传播

如果我们用JAX替换掉了NumPy：

1
import jax.numpy as np

那么计算梯度也变得很简单：

1
2
3
4
5
6
7
def lm_loss(params, inputs, n_head) -> float:
    x, y = inputs[:-1], inputs[1:]
    output = gpt2(x, **params, n_head=n_head)
    loss = np.mean(-np.log(output[y]))
    return loss

grads = jax.grad(lm_loss)(params, inputs, n_head)

批处理

还是那句话，如果我们用JAX替换掉NumPy[7]：

1
import jax.numpy as np

那么让gpt2函数批量化就变得很简单：

1
2
3

gpt2_batched = jax.vmap(gpt2, in_axes=[0, None, None, None, None, None])
gpt2_batched(batched_inputs) # [batch, seq_len] -> [batch, seq_len, vocab]

推断优化

我们的实现相当低效。除了支持GPU和批处理之外，最快且最有效的优化可能是实现一个键值缓存。此外，我们顺序地实现了注意力头计算，而实际上我们应该使用并行计算[8]。

其实还有很多很多的推理优化可以做。我建议从Lillian Weng的Large Transformer Model Inference Optimization和Kipply的Transformer Inference Arithmetic开始学习。

译者注：循循善诱，拉你入坑可还行

训练

训练 GPT 对于神经网络来说是非常标准的行为（针对损失函数进行梯度下降）。当然，在训练 GPT 时你还需要使用一堆常规的技巧（使用 Adam 优化器，找到最佳的学习率，通过dropout和/或权重衰减进行正则化，使用学习率规划器，使用正确的权重初始化，进行分批处理等等）。

而训练一个好的GPT模型的真正秘诀在于能够扩展数据和模型，这也是真正的挑战所在。

为了扩展数据量，您需要拥有大规模、高质量、多样化的文本语料库。

  • 大规模意味着拥有数十亿的token（数百万GB的数据）。例如可以查看The Pile，这是一个用于大型语言模型的开源预训练数据集。
  • 高质量意味着需要过滤掉重复的示例、未格式化的文本、不连贯的文本、垃圾文本等等。
  • 多样性意味着序列长度变化大，涵盖了许多不同的主题，来自不同的来源，具有不同的观点等等。当然，如果数据中存在任何偏见，它将反映在模型中，因此您需要谨慎处理。

将模型扩展到数十亿个参数需要超级大量的工程（和金钱lol）。训练框架会变得非常冗长和复杂。关于这个主题的一个良好起点是Lillian Weng的How to Train Really Large Models on Many GPUs。当然，关于这个话题还有NVIDIA的Megatron Framework, Cohere的训练框架, Google的PALM, 开源的mesh-transformer-jax（用于训练EleutherAI的开源模型），以及很多、很多、很多。

评估

哦对了，那么要怎么评估大语言模型呢？老实说，这是一个非常困难的问题。HELM 是一个相当全面且不错的起点，但你应该始终对基准测试和评估指标保持怀疑的态度。

架构改进

我推荐看一下Phil Wang的X-Transformers。它包含了Transformer架构的最新最赞的研究。这篇论文也是一个不错的概述(见表格1)。Facebook最近的LLaMA论文也可能是标准架构改进的一个很好的参考（截至2023年2月）。

译者注：学transformer的小伙伴，看完x-transformers绝对功力大涨

停止生成

我们当前的实现需要事先指定要生成的确切token数量。这不是一个很好的方法，因为我们生成的文本可能会太长、太短或在句子中间截断。

为了解决这个问题，我们可以引入一个特殊的句子结束（EOS）token。在预训练期间，我们在输入的末尾附加EOS token（比如，tokens = ["not", "all", "heroes", "wear", "capes", ".", "<|EOS|>"]）。在生成过程中，我们只需要在遇到EOS token时停止（或者达到最大序列长度）：

1
2
3
4
5
6
7
def generate(inputs, eos_id, max_seq_len):
	prompt_len = len(inputs)
	while inputs[-1] != eos_id and len(inputs) < max_seq_len:
        output = gpt(inputs)
        next_id = np.argmax(output[-1])
        inputs.append(int(next_id))
    return inputs[prompt_len:]

GPT-2 没有使用 EOS token进行预训练，因此我们无法在我们的代码中使用这种方法，但是现在大多数 LLMs 都已经使用 EOS token了。

无条件生成

使用我们的模型生成文本需要对其提供提示条件。但是我们也可以让模型执行无条件生成，即模型在没有任何输入提示的情况下生成文本。

这是通过在预训练期间在输入开头加上一个特殊的句子开头（BOS）token来实现的（例如 tokens = ["<|BOS|>", "not", "all", "heroes", "wear", "capes", "."]）。要进行无条件文本生成的话，我们就输入一个仅包含BOS token的列表：

1
2
3
4
5
6
7
def generate_unconditioned(bos_id, n_tokens_to_generate):
	inputs = [bos_id]
    for _ in range(n_tokens_to_generate):
        output = gpt(inputs)
        next_id = np.argmax(output[-1])
        inputs.append(int(next_id))
    return inputs[1:]

GPT-2的预训练是带有BOS token的（不过它有一个令人困惑的名字<|endoftext|>），因此在我们的实现中要运行无条件生成的话，只需要简单地将这行代码更改为：

1
input_ids = encoder.encode(prompt) if prompt else [encoder.encoder["<|endoftext|>"]]

然后运行;

1
python gpt2.py ""

然后即可生成：

1
The first time I saw the new version of the game, I was so excited. I was so excited to see the new version of the game, I was so excited to see the new version

因为我们使用的是贪心采样，所以输出结果不是很好（重复的内容较多），且每次运行代码的输出结果都是确定的。为了获得更高质量的、不确定性更大的生成结果，我们需要直接从概率分布中进行采样（最好在使用top-p之类的方法后进行采样）。

无条件生成不是特别有用，但它是演示GPT能力的一种有趣方式。

微调

我们在训练部分简要介绍了微调。回想一下，微调是指我们复用预训练的权重，对模型在某些下游任务上进行训练。我们称这个过程为迁移学习。

理论上，我们可以使用零样本或少样本提示来让模型完成我们的任务，但是如果您可以访问一个标注的数据集，对GPT进行微调将会产生更好的结果（这些结果可以在获得更多数据和更高质量的数据时进行扩展）。

好的，以下是关于微调的一些相关主题：

分类微调

在分类微调中，我们会给模型一些文本，并要求它预测它属于哪个类别。以IMDB数据集为例，它包含着电影评论，将电影评为好或坏：

1
2
3
4
5
6
7
8
--- Example 1 ---
Text: I wouldn't rent this one even on dollar rental night.
Label: Bad
--- Example 2 ---
Text: I don't know why I like this movie so well, but I never get tired of watching it.
Label: Good
--- Example 3 ---
...

为了微调我们的模型，我们需要用分类头替换语言建模头，将其应用于最后一个token的输出：

1
2
3
4
5
6
7
8
9
10

def gpt2(inputs, wte, wpe, blocks, ln_f, cls_head, n_head):
    x = wte[inputs] + wpe[range(len(inputs))]
    for block in blocks:
        x = transformer_block(x, **block, n_head=n_head)
    x = layer_norm(x, **ln_f)

	# project to n_classes
	# [n_embd] @ [n_embd, n_classes] -> [n_classes]
    return x[-1] @ cls_head

这里我们只使用最后一个token的输出x[-1]，因为我们只需要为整个输入产生一个单一的概率分布，而不是像语言模型一样产生n_seq个分布。我们特别选择最后一个token（而不是第一个token或所有token的组合），因为最后一个token是唯一允许关注整个序列的token，因此它具有关于整个输入文本的信息。

同往常一样，我们根据交叉熵损失进行优化：

1
2
3
4
5
def singe_example_loss_fn(inputs: list[int], label: int, params) -> float:
    logits = gpt(inputs, **params)
    probs = softmax(logits)
    loss = -np.log(probs[label]) # cross entropy loss
    return loss

我们还可以执行多标签分类（即一个样本可以属于多个类别，而不仅仅是一个类别），这可以通过使用sigmoid替代softmax并针对每个类别采用二分交叉熵损失（参见这个stackexchange问题）。

生成式微调

有些任务无法被简单地认为是分类，如摘要的任务。我们可以通过对输入和标签拼接进行语言建模，从而实现这类任务的微调。例如，下面就是一个摘要训练样本的示例：

1
2
3
4
--- Article ---
This is an article I would like to summarize.
--- Summary ---
This is the summary.

我们就像预训练时那样训练这个模型（根据语言建模的损失进行优化）。

在预测时，我们将直到"--- Summary ---"的输入喂给模型，然后执行自回归语言建模以生成摘要。

定界符"--- Article ---"和"--- Summary ---"的选择是任意的。如何选择文本格式由您决定，只要在训练和推断中保持一致即可。

请注意，其实我们也可以将分类任务表述为生成任务（以IMDB为例）：

1
2
3
4
--- Text ---
I wouldn't rent this one even on dollar rental night.
--- Label ---
Bad

然而，这种方法的表现很可能会比直接进行分类微调要差（损失函数包括对整个序列进行语言建模，而不仅仅是对最终预测的输出进行建模，因此与预测有关的损失将被稀释）。

指令微调

目前大多数最先进的大型语言模型在预训练后还需要经过一个额外的指令微调步骤。在这个步骤中，模型在成千上万个由人工标注的指令提示+补全对上进行微调（生成式）。指令微调也可以称为监督式微调，因为数据是人工标记的（即有监督的）。

那指令微调的好处是什么呢？虽然在预测维基百科文章中的下一个词时，模型在续写句子方面表现得很好，但它并不擅长遵循说明、进行对话或对文件进行摘要（这些是我们希望GPT能够做到的事情）。在人类标记的指令 + 完成对中微调它们是教导模型如何变得更有用，并使它们更容易交互的一种方法。我们将其称为AI对齐(AI alignment)，因为我们需要模型以我们想要的方式做事和表现。对齐是一个活跃的研究领域，它不仅仅只包括遵循说明（还涉及偏见、安全、意图等）的问题。

那么这些指令数据到底是什么样子的呢？Google的FLAN模型是在多个学术的自然语言处理数据集（这些数据集已经被人工标注）上进行训练的：

(fig 3)

来自FLAN论文的图3

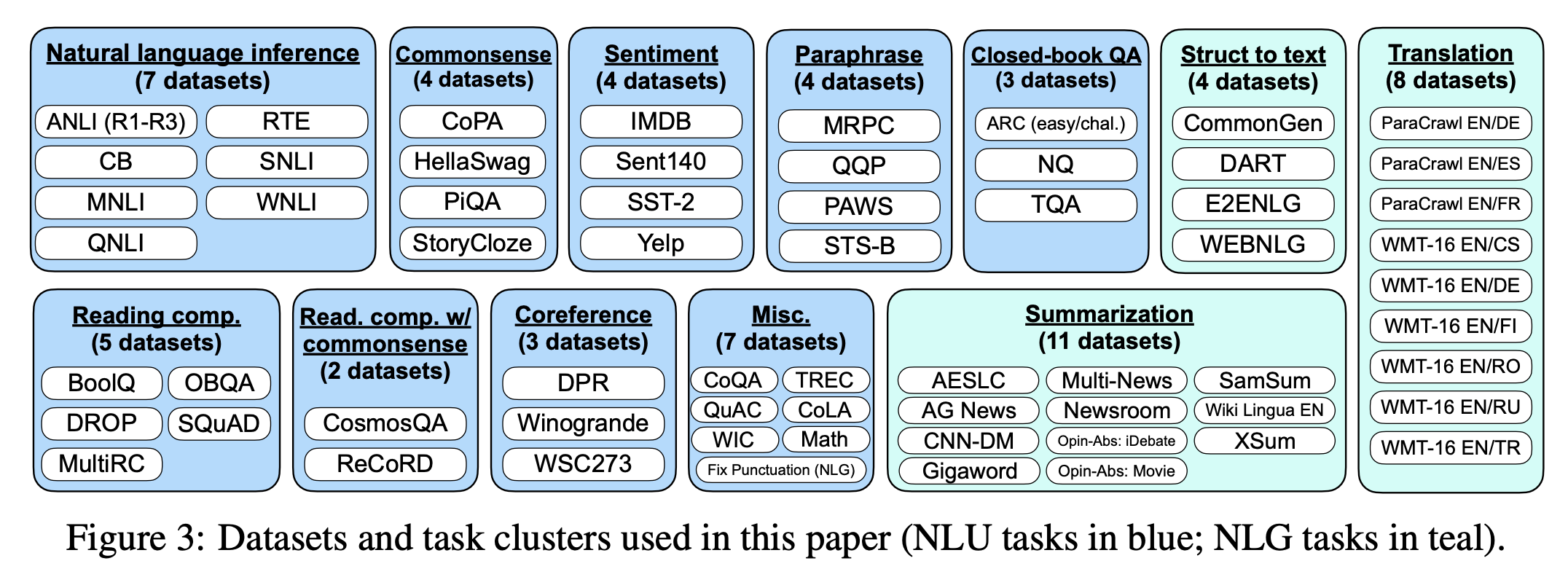
OpenAI的InstructGPT则使用了从其API中收集的提示进行训练。然后他们雇佣工人为这些提示编写补全。下面是这些数据的详细信息：

(igpt)

来自InstructGPT论文的表1与表2

参数高效微调（Parameter Efficient Fine-tuning）

当我们在上面的部分讨论微调时，我们是在更新模型的所有参数。虽然这可以获得最佳性能，但成本非常高，无论是在计算方面（需要经过整个模型进行反向传播），还是在存储方面（对于每个微调的模型，您需要存储完一份全新的参数副本）。

最简单的解决方法是只更新模型头部并冻结（即使其不可训练）模型的其它部分。虽然这样做可以加速训练并大大减少新参数的数量，但其表现并不好，因为某种意义上我们损失了深度学习中的深度。相反，我们可以选择性地冻结特定层（例如冻结除了最后四层外的所有层，或每隔一层进行冻结，或冻结除多头注意力参数外的所有参数），那么这将有助于恢复深度。这种方法的性能要好得多，但我们也变得不那么参数高效(parameter efficient)，同时也失去了一些训练速度的优势。

除此之外，我们还可以利用参数高效微调(Parameter Efficient Fine-tuning)方法。这仍然是一个活跃的研究领域，有许多不同的方法可供选择、选择、选择、选择、选择、选择、选择。

举个例子，我们可以看看Adapters论文。在这种方法中，我们在transformer模块的FFN和MHA层后添加了一个额外的“adapter”层。这里的adapter层只是一个简单的两层全连接神经网络，其中输入和输出维度是n_embd，而隐藏维度小于n_embd：

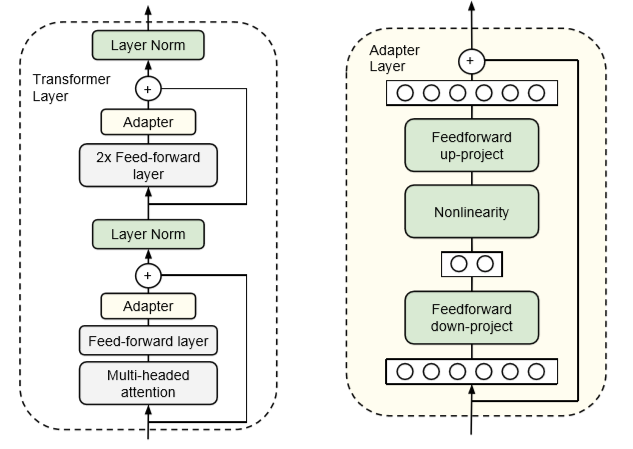
(adapter)

来自Adapters论文的图2

适配器方法中，隐藏层的大小是一个我们可以设置的超参数，这使我们能够在参数和性能之间进行权衡。该论文表明，对于BERT模型，使用这种方法可以将训练参数数量降低到2％，而与完全微调相比仅有少量的性能下降(<1%)。

  1. 1.大规模训练、收集海量数据、提高模型速度、性能评估以及对齐模型使其为人类服务，数百名工程师/研究人员的将这视为终身事业，这些人的工作造就了今时今日的大型语言模型，绝不仅仅是因为模型的架构。GPT架构恰好是第一个具有良好的可扩展性、可在GPU上高度并行化且善于序列建模的神经网络架构。真正的秘诀来自于扩展的数据和模型规模（一如既往的重要），GPT只是让我们可以这样做而已[9]。可能Transformer的成功是刚好中了硬件彩票而已，还有一些其他的架构可能正在等待着取代Transformer。 ↩
  2. 2.对于某些应用程序，分词器不需要一个decoder方法。例如，如果你想要对电影评论进行分类，判断评论是说这部电影好还是不好，你只需要能够对文本进行encode，并在模型上进行前向传递，没有必要进行decode。但是对于生成文本，decode是必需的。 ↩
  3. 3.虽然有InstructGPT和Chinchilla的论文，我们已经意识到实际上并不需要训练那么大的模型。在经过最优训练和指令微调后，参数为13亿的GPT模型可以胜过参数为1750亿的GPT-3。 ↩
  4. 4.原始的transformer论文使用了预计算的位置嵌入（positional embedding），他们发现这种方法的表现和学习的位置嵌入一样好，但其有一个明显的优势，即你可以输入任意长的序列（不受最大序列长度的限制）。然而在实践中，您的模型只能表现得和它所训练的序列长度一样好。您不能只在长度为1024的序列上训练GPT，然后指望它在长度为16k的序列上表现良好。然而最近出现了一些成功的相对位置嵌入（relative positional embeddings）方法，如Alibi和RoPE。 ↩
  5. 5.不同的GPT模型可能选择不同的隐藏层宽度，而不必是4*n_embd，这是GPT模型的通行做法。此外，我们在推动Transformer的成功方面给予多头注意力层很多注意（双关了哦～），但在GPT-3的规模下，80%的模型参数包含在前馈层中。这是值得思考的事情。 ↩
  6. 6.如果你还没有被说服，可以看一下softmax方程，自己琢磨一下这是正确的（甚至可以拿出笔和纸进行计算）。 ↩
  7. 7.表白JAX ↩
  8. 8.使用JAX的话，这就可以简单写为heads = jax.vmap(attention, in_axes=(0, 0, 0, None))(q, k, v, causal_mask) ↩
  9. 9.实际上，我可能会争辩一下注意力模型在处理序列时的方式与循环/卷积层相比，具有内在的优越性，但现在我们已经陷入了一个注脚中的注脚了，那还是先打住吧。 ↩